Carapace Protocol
Decentralized Protection Against Credit Default Risk
Taisuke Mino
Abstract
This paper proposes decentralized protection against default risk in under-collateralized crypto loans. Traditionally, protection against credit default risk is known as credit default swaps.
We aim to build the next DeFi primitive currently missing in the market to make DeFi more resilient to credit risks. Credit risk protection is critical for the mass adoption of decentralized finance.
We create a market where traders can swap the default risk. Protection buyers pay a premium to get the right to claim protection when an underlying loan defaults. Protection sellers provide capital for protection in exchange for a premium. When a default event occurs, a payout is made to protection buyers.
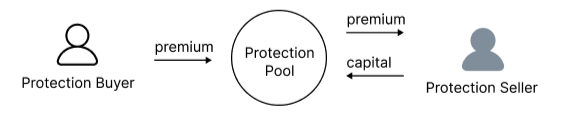
Carapace protocol is a non-custodial automated market maker implemented on a blockchain. Our automated market maker (AMM) pools liquidity and makes it available to swap traders according to an algorithm such as our premium pricing formula that fluctuates with supply and demand and the exchange rate formula that keeps increasing with the interest accrual.
Peer-to-Pool Model
Each swap market is represented by a pool contract.
Pool Design
Each pool contract represents a bundle of lending pools in under-collateralized lending protocols such as Goldfinch, Maple Finance, TrueFi, to name a few. We aggregate lending pools across these lending protocols for diversification and liquidity.
Protection Buyers
If you want to hedge against the default risk of a specific underlying lending pool, you can pay some premium to a pool contract and get the right to claim a payout if the lending pool defaults.
Protection Sellers
If you are convinced that the underlying lending pools are safe, you can invest capital in the respective pool contract to earn yields. You will get a representative sToken in exchange for the capital you have invested.
If one of the lending pools defaults, some liquidity is kept aside for protection. If no loan defaults within the designated period, then protection sellers earn yield via premium payment, without facing any loss.
Our pool contract locks the capital provided for some time to prevent protection sellers from running away without providing protection when a lending pool defaults.
Sellers can always request to withdraw the deposited capital, or they can keep their capital in a pool to keep earning yields.
Premium Pricing
premium = (carapace_risk_premium + underlying_risk_premium) * protection_amount
Carapace Risk Premium
carapace_risk_premium
= max((1 - (e ** (- duration * risk_factor))), MIN_CARAPACE_RISK_PREMIUM )
e is the mathematical constant. We use the e because we assume survival of the protections in the protection pool follows the Poisson distribution.
carapace_risk_premium is priced based on three main factors:
- 1. duration which is selected by protection buyers.
- 2. risk_factor, which represents how risky a given pool is. It simulates the hazard rate(survival rate or (1 - default rate)) in the Poisson distribution.
- 3. MIN_CARAPACE_RISK_PREMIUM is the minimum amount of carapace_risk_premium paid by a protection buyer.
We will explain them in more detail below.
Duration
duration is the expiration time minus the current time. All other things being equal, the premium is cheaper when the duration is shorter because it is less likely that a default event occurs when there is a shorter window of time for loans to default.
Since traders typically work with days remaining to expiration, we convert these to the percentage of the year. For example, for protection that expires in 10 days, the duration input is 10/365.24 = 0.0273 or 2.73%.
To sum up, we can express the duration with:
days_to_expiration / 365.24
Risk Factor
The risk factor represents how the market thinks about the risk of a particular pool. The riskier the pool, the higher the risk factor and the more expensive a premium becomes. A risk factor of 1 means a pool is quite risky, while a risk factor of 0 means a pool is quite safe.
risk_factor
= (((LEVERAGE_RATIO_CEILING + BUFFER) - leverage_ratio) /
(leverage_ratio - (LEVERAGE_RATIO_FLOOR - BUFFER)))
* CURVATURE
The risk factor is calculated based on two main factors:
- 1. leverage_ratio which fluctuates with changes in supply and demand in the market
- 2. CURVATURE which is determined by the core team (and eventually by our community).
We will explain the two main factors below in detail.
Leverage Ratio
Here, we will be explaining the first part of the risk factor equation:
(((LEVERAGE_RATIO_CEILING + BUFFER) - leverage_ratio) /
(leverage_ratio - (LEVERAGE_RATIO_FLOOR - BUFFER)))
Our protection pool is leveraged; the pool doesn’t store capital for the total protection amount because it is unlikely that all the protected loans are going to default at the same time. The leverage ratio is calculated with the equation below.
the leverage ratio = total_sToken_underlying / total_protection_amount
where
total_sToken_underlying = seller_deposit + accrued_premiums - default_payouts
The higher the leverage ratio is, the lower the risk factor and the premium are because the market believes that underlying loans are safe. The lower the leverage ratio is, the higher the risk factor and the premium are because the market believes that underlying loans are unsafe. You can see the graph below where the premium price is plotted depending on the leverage ratio(this is for reference only).
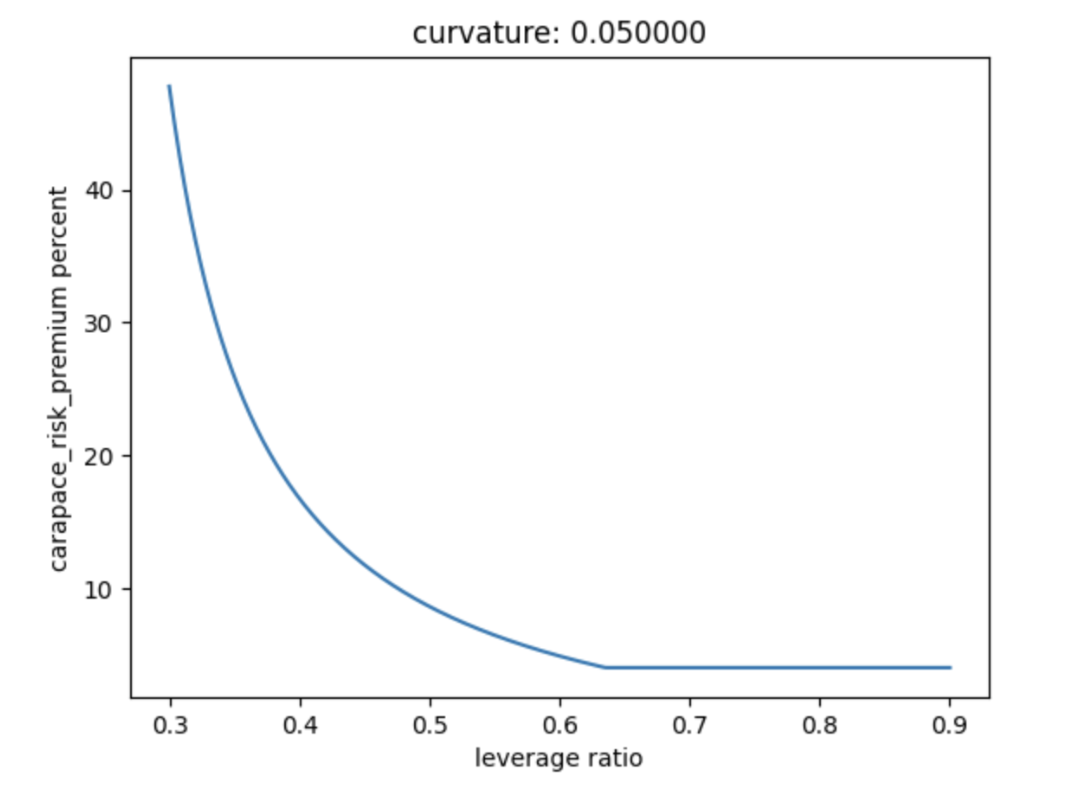
When there is more demand, the total_protection_amount value increases more than the accrued_premiums value, which means the leverage ratio goes down. Thus, with the higher demand, the risk factor and the premium will be higher.
When there is more supply, the sToken underlying amount increases, which means the leverage ratio increases. Thus, with a higher supply, the risk factor and the premium will be lower.
As you can see, the premium price is effectively an aggregated view of supply and demand in the market. In other words, the premium price is the prediction of the market about default risk.
Lastly, we use the buffer value(e.g. 0.05) to avoid edge case inconsistency. For example, when the leverage ratio goes to the floor, without subtracting the buffer value, the premium curve steepens at a high pace and goes to 100%. The buffer values also ensure that the numerator or denominator won’t be zero.
Curvature
CURVATURE exists literally to adjust the curvature of the curve. If this doesn’t exist or if this is 1, the shape would be linear. 0.01 is steeper than 0.05.
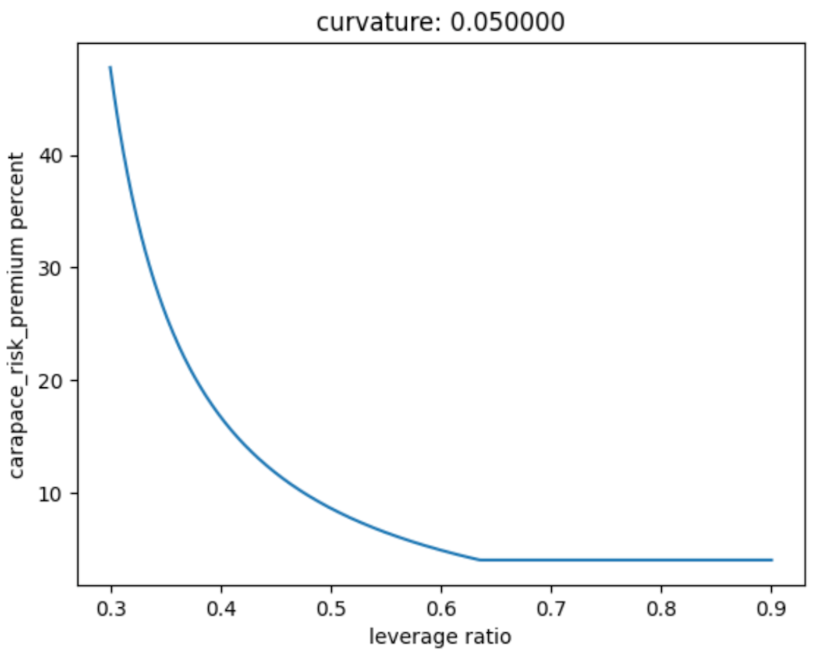
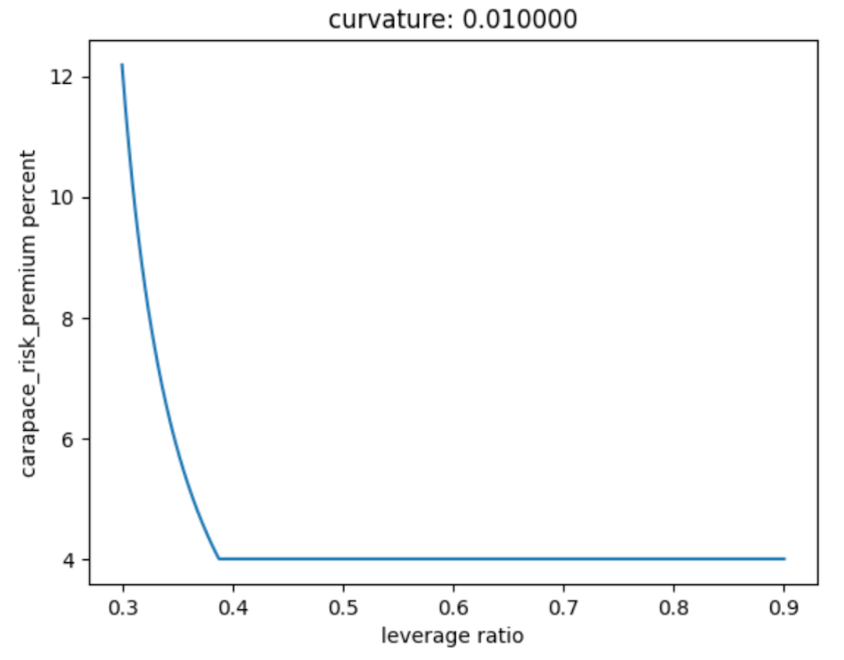
Minimum Carapace Risk Premium
The MIN_CARAPACE_RISK_PREMIUM is the minimum carapace_risk_premium paid by a protection buyer regardless of the leverage ratio.
Underlying Risk Premium
The underlying_risk_premium represents the level of risk in an underlying lending pool within a given protection pool. The riskier the underlying lending pools are, the more expensive the underlying_risk_premium. We use the yield from underlying lending pools to indicate the level of risk; for lenders of unsecured lending protocols, higher yields indicate a higher risk of default.
underlying_risk_premium
= UNDERLYING_RISK_PREMIUM_PERCENT * duration * protection_buyer_apy
UNDERLYING_RISK_PREMIUM_PERCENT is a constant value like 10% which represents the percentage of protection buyers yields we take into account.
duration is the expiration time minus the current time as we explained in the Carapace Risk Premium section.
protection_buyer_apy is the expected yield for protection buyers in underlying lending pools. The higher the protection_buyer_apr is, the higher the risk of underlying loans and the premium are.
Protection Amount
The amount of protection a buyer wants to get. protection_amount is selected by protection buyers. The more protection you want to get, the more premium you need to pay.
Yields Distribution
Carapace Protocol distributes yields with a combination of 1) an sToken in each pool, 2) the exchange rate, and 3) the accrued premium.
sToken
sToken is an interest-bearing token that protection sellers get in exchange for an underlying token like USDC that they deposit. Each pool represents a different risk and has its sToken.
The sToken represents the capital provided plus interest from the premium (we will also source interest from rehypothecation in upcoming versions).
Protection sellers can return their sToken to redeem their deposited capital and interest once the lockup period has ended. The sToken will be burned when sellers withdraw their capital. Some capital and interest may be lost due to a default event.
If sellers wish to redeem their capital and interest before the lockup period, they might be able to find a buyer of their sToken in a secondary market like Uniswap. Traders in the exchanges can long/short sTokens based on their opinion about the risk exposure associated with sTokens. Since an sToken is a fungible ERC20 token, it is fairly easy to bootstrap the secondary markets for protection sellers.
The Exchange Rate
The exchange rate is the total sToken underlying token amount divided by the total supply of sTokens.
the exchange rate = total_sToken_underlying / total_sTokens
You can get the total underlying value of the total sToken by multiplying the total sTokens with the exchange rate.
total_sToken_underlying = total_sTokens * the_exchange_rate
where total_sToken_underlying
= total_seller_deposit + total_accrued_premiums - total_default_payouts(if any)
You can get your share of underlying tokens by multiplying your sToken share with the exchange rate.
Although an sToken amount stays constant, the token accumulates interest through the exchange rate; the exchange rate keeps increasing as a premium is paid by protection buyers. Thus, each sToken is exchangeable with an increasing amount of its underlying token. In other words, the interest for each sToken holder is the delta between the sToken * the exchange rate when they exit the market and the sToken * the exchange rate when they enter the market. The exchange rate decreases only when the capital is locked for potential default claim payouts.
Mathematically speaking, the exchange rate changes only when total_accrued_premiums or total_default_payouts change, which means only when there are premium accrual or default payouts. The exchange rate doesn’t change with the seller's deposit or withdrawal amount because the sTokens minted and sTokens burned will be proportional to the deposited or withdrawn amount. The protection purchase doesn’t also change the exchange rate at that block because there is no premium accrued for that protection yet.
One key property of the exchange rate is that the exchange rate from time A to B and B to C is the same as the exchange rate from A to C. If we calculate the exchange rate at time C from time A, we get the same exchange rate when we calculate the exchange rate at time B from time A and then calculate the exchange at time C from time B. In both ways, the exchange rate at C will be the same.
Accrued Premium
As we discussed above,
the exchange rate = total_sToken_underlying / total_sTokens
where
total_sToken_underlying
= total_seller_deposit + total_accrued_premiums - total_default_payouts(if any)
The total_seller_deposit is self-explanatory. The total_default_payouts is the amount of capital locked for potential default claim payouts.
The biggest question is how we calculate the total_accrued_premiums. In short, the premium paid by a buyer will accrue for sellers over the duration of protection.
Accrued premium AP between any time t and T:
AP = K * ( - )
We will explain the premium accrual in more detail below. Accrued premium is priced based on three main factors:
- 1. K is a constant amount that acts like a unit.
- 2. t is the beginning time and T is the end time of protection.
- 3. 𝜆 is the risk factor from the premium pricing formula for this protection divided by 365.
K
K = P / ( - )
where P is premium protocol_fees.
Imagine that a protection buyer has bought 180 days protection for $10,000 and the protocol fee is $100. Then:
K = (10,000 - 100) / (1 - )
t and T
t is the beginning time and T is the end time of protection. In other words, duration is T - t.
where: 0 < t < T
t and T can be seconds as long as they are expressed in years. This is because we use 365 in the risk factor below.
𝜆
𝜆 is the risk factor from the premium pricing formula for this protection divided by 365 (we use 365 regardless of the duration to get units in years). We assume risk follows Poisson distribution in line with premium pricing.
𝜆
= risk_factor / 365
= (((LEVERAGE_RATIO_CEILING + BUFFER) - leverage_ratio)
/ (leverage_ratio - (LEVERAGE_RATIO_FLOOR - BUFFER)))
* CURVATURE / 365
Example
Imagine that a protection buyer has bought 180 days protection for $10,000 and the protocol fee is $100. The premium for the pool is paid on day 0, and the protection covers till day 180. How do we calculate the accrued premium after 180 days?
K = (10,000 - 100) / (1 - )
Accrued premium(AP) from day 0 to day 180
= K * ( - )
= K * ( 1 - )
We can also say that the accrued premium for day 0 + day 1 + day 2 + … + day 180
= K * ( - )
Transitivity
The accrued premium has a transitive property. Accrued premium from time A to C = Accrued premium from time A to B + accrued premium from time B to C.
Fair Distribution
One of the most important principles of yield distribution is fairness. I will outline how we distribute yield fairly with the above distribution mechanism.
First, at the risk of stating the obvious, a protection seller is entitled to receive a premium only when they protect protection buyers. Thus, protection sellers get a premium only when their locking period overlaps with the protection duration of protection buyers. This is why we accrue a premium over the duration of protection following the Poisson distribution. Second, when a seller withdraws, they get a proportional amount of premium depending on their share of total capital provided in a given block. Third, the longer they keep their capital in a pool, the more premium they can earn. They can earn more interest with the longer deposit term because the delta between the sToken the exchange rate when they exit the market and the sToken the exchange rate when they enter the market will be bigger.
Security
We take security seriously to maintain trust in our system.
Insolvency
Leverage Ratio Floor
We will take a conservative approach to our leverage ratio floor initially. In traditional insurance, big insurance companies' leverage ratio can be as low as 2%. We will start conservatively and adjust the ratio as our community accumulates information and knowledge.
Incentives
In the case of a bank run, the leverage ratio goes down, and the interest rates go up. As a result, there is an incentive 1) to bring more liquidity with new money and 2) for the existing money to stay invested.
We also plan to reward CARA tokens to sellers when the leverage ratio is below the floor.
Backstop Treasury Funds
Our protocol earns some fees, and some of our revenue stored in our treasury contract will be used as a backstop. Also, Starlings Lab (an R&D company behind Carapace) might provide some backstop capital.
CARA Token Backstop
We will reserve a portion of CARA token allocation as a backstop to cover even more loss.
Frauds
In traditional CDS, concern has been expressed about the manipulation of underlying loans. For example, a CDS buyer may pay a borrower to default. We have a defense mechanism to mitigate this classic insurance risk. In short, we require protection buyers to be a lender of an underlying loan with our proof of loss system.
Proof of Loss
More specifically, at the point of default claiming, our proof of loss system requires protection buyers to lock the LP tokens that represent a loan amount in under-collateralized lending protocols. In this way, only a lender can be a protection buyer, and a protection buyer can get only what they have lost. In other words, we support only non-naked-CDS.
Imagine that our protocol supports naked CDS that allows anybody to be a buyer without lending money in underlying loans. This CDS design strongly incentivizes borrowers to default because they can earn their borrowing amount plus the protection payout without lending any money.
There are two possible attacks against this system where a protection buyer who is also a lender in an underlying loan manipulates a default event.
First, self-loan. Let's say Bob lends $10k to himself as an LP and borrows $100k in total. Bob pays a premium to Carapace to get $10k worth of protection. He maliciously defaults and keeps $100k + $10k - premium. Second, collusion between a lender and a borrower. Bob(LP) lends $10k to Alice(borrower). Alice borrows $100k in total. Bob pays a premium to Carapace to get $10k worth of protection. Alice maliciously defaults. Bob and Alice collectively keep $100k + $10k - premium.
Legit under-collateralized lending protocols have a security model against these attacks. Most importantly, borrowers are required to go through the KYC process. It goes without saying that Bob and Alice face significant reputation risk that damages their reputation widely and serious legal risk of getting arrested in both cases as long as there is an identity system. Some protocols, such as Goldfinch have another layer of protection where a randomly chosen auditor carefully chooses a borrower who is not involved in collusion. Sure, there is no perfect guard against this exploitation in underlying protocols because it can be difficult to prove collusion between a borrower and a lender. However, their security model does make collusion much more difficult.
It is critical for the community to review each under-collateralized lending protocol rigorously and ensure that they have the right security model.
Default Payouts
Protection buyers get protection depending on how much premium they have paid, and they get only what they have lost. After a claim is made, our contract verifies protection purchases with underlying LP tokens and the buyer’s address. When verification is successful, the payout is made to the buyer in the same transaction.
Payouts Funds Source
Default payouts will be funded by the following sources (in this order):
- 1. Non-accrued premium of defaulted underlying loans
- 2. Underlying amount of sTokens including accrued premium
- 3. Backstop treasury funds
- 4. Other non-accrued premium
- 5. CARA token backstop
The accrued premium is the allocated portion of the premium that has already been distributed to sellers. The non-accrued premium is the premium that has been collected from buyers but is yet to be allocated to sellers. The non-accrued premium of the defaulted underlying loans from the claiming buyer should be used first because this capital is supposed to be distributed to the protection sellers who are facing defaulted underlying loans. The other non-accrued premium should not be used until other capital is depleted. Otherwise, protection sellers have no incentive to keep their capital in a pool.
Dispute Resolution
The Carapace protocol does its best to clearly define what constitutes a default event, as explained above. We also plan to set up a committee with disinterested parties as a dispute resolution mechanism. In case our contract cannot algorithmically determine if the default happened or not due to unexpected events such as smart contract hacking and other things that we do not even know yet, the committee comes in. The committee is made up of members of the core team of Carapace as well as credit advisors to Carapace. Committee members should not participate in the market to avoid conflict of interest. When there is a dispute, the committee evaluates a claim with a vote. This committee uses a multi-sig contract that accepts or denies a dispute submission. All of the members of the committee have a stake in Carapace and an interest in doing what's best for the long-term success of Carapace. In other words, they have skin in the game because their wrong decision will make them suffer economically.
Acknowledgments
Special thanks to Rohit Sabnis, Sabir Shaik, and Vipul Nadoda for ideas, heavy feedback, and brainstorming help when writing this. The paper would not have been possible without them.
Disclaimer
This paper is for general information purposes only. It does not constitute investment advice or a recommendation or a solicitation to buy or sell any investment and should not be used in the evaluation of the merits of making any investment decision. It should not be relied upon for accounting, legal or tax advice or investment recommendations. The opinions reflected herein are subject to change without being updated.

